2020-07-10

OpenGL 筆記 - Transform

前面講了 Shader 跟 Texture 都是外觀的表現，但這些都是靜態的圖像，那在 OpenGL 要怎麼讓圖像動起來呢?當然，你可以每一幀都重新配置 VBO ，但這太消耗資源了，更好的方法是用 矩陣(Matrix) 將座標 轉換(Transform) 過去

向量 Vector

方向，由方向和大小組成

$\bar{v} = \begin{pmatrix} \color{red}x \\ \color{green}y \\ \color{blue}z \end{pmatrix}$

$\vec{v} = \vec{w}$
標量 Scalar
- 不能反過來
- $\begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + x = \begin{pmatrix} \color{red}1 + x \\ \color{green}2 + x \\ \color{blue}3 + x \end{pmatrix}$
反向
- $-\bar{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}$
向量加法
- $\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + \bar{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}$
向量減法
- $\bar{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \bar{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \bar{v} + -\bar{k} = \begin{pmatrix} \color{red}1 + (-\color{red}{4}) \\ \color{green}2 + (-\color{green}{5}) \\ \color{blue}3 + (-\color{blue}{6}) \end{pmatrix} = \begin{pmatrix} -\color{red}{3} \\ -\color{green}{3} \\ -\color{blue}{3} \end{pmatrix}$
長度
- $||\color{red}{\bar{v}}|| = \sqrt{\color{green}x^2 + \color{blue}y^2}$
單位向量
- 長度 = 1
- 標準化 (Normalize)
- 任意向量除以其長度 = 單位向量
- $\hat{n} = \frac{\bar{v}}{||\bar{v}||}$

內積 (Dot product)

定義
- $\vec{a} \cdot \vec{b} = \vert\vec{a}\vert \vert \vec{b}\vert cos\theta$
一些性質
- $cos \theta = \frac{\vec{a} \cdot \vec{b}}{\vert\vec{a}\vert \vert \vec{b}\vert}$
- 單位向量內積: $\bar{v} \cdot \bar{k} = 1 \cdot 1 \cdot \cos \theta = \cos \theta$
  - 可以求兩向量夾角
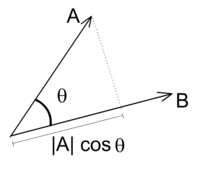
投影
- a 純量投影投影到 b 上: $a_b = \vert \vec{a} \vert cos\theta$
  - $\vec{a} \cdot \vec{b} = a_b \vert \vec{b} \vert = b_a \vert \vec{a} \vert$

計算
- 把每個分量相乘
- 用反餘弦 $\cos^{-1}$ 可以求得向量夾角
- e.g.

外積 (Cross product)

用來求與兩向量垂直的向量之方向，在計算三維空間中平面的垂直方向。

$\vert a\times b \vert = \vert a \vert \vert b \vert sin \theta$
- $0^\circ < \theta < 180^\circ$
計算
$\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}} \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}$

矩陣 Matrix

$m\times n$ 的矩形陣列，裏頭的元素可以是數字、符號或算式。

$\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}$

加法、減法
- Scalar (glm)
  - $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \color{green}3 = \begin{bmatrix} 1 + \color{green}3 & 2 + \color{green}3 \\ 3 + \color{green}3 & 4 + \color{green}3 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 6 & 7 \end{bmatrix}$
  - $\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} - \color{green}3 = \begin{bmatrix} 1 - \color{green}3 & 2 - \color{green}3 \\ 3 - \color{green}3 & 4 - \color{green}3 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 0 & 1 \end{bmatrix}$
- 矩陣加減
  - $\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}$
  - $\begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2 - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}$
Scalar 標量乘法
- $\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}2 \cdot 1 & \color{green}2 \cdot 2 \\ \color{green}2 \cdot 3 & \color{green}2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}$
矩陣乘法
- $M_{a\times b} \cdot M_{c\times d}$ 只有 $b = c$ 才可以相乘，產出 $M_{a\times d}$
- 沒有交換律，$A \cdot B \neq B \cdot A$

$$
\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}
$$

運算規則
- 交換律
  - $A+B = B+A$
- 分配律
  - $(A+B)^T = A^T + B^T$ 轉置
  - $n(A+B) = nA+nB$ 純量乘法
- $n(A^T) = (nA)^T$
單位矩陣 Identity Matrix
- 除了對角線之外都是 $0$

$$
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}
$$

縮放 Scale
- $S_1 = S_2 = S_3$ 稱作均勻縮放(Uniform Scale)

$$
\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}
$$

位移 Translate
- 原始向量加上另一個向量，移動了原始向量
- 位移向量 $(T_x, T_y, T_z)$

$$
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}
$$

所以的位移值($T_x, T_y, T_z$)都會乘上 $w$，$w$ 稱作齊次座標(Homogeneous Coordinates)，它讓我們可以用矩陣乘法來表示向量位移

旋轉 (Rotation)

旋轉會有角(Angle)，而角可以用角度(Degree)及弧度(Radian)表示，角度比較直觀，但電腦計算通常都用弧度

互換
- 弧度轉角度
  - 角度 = 弧度 * (180.0f / PI)
- 角度轉弧度
  - 弧度 = 角度 * (PI / 180.0f)

在 3D 空間中旋轉需要:角(Angle)跟旋轉軸(Rotation Axis)

沿 x 軸旋轉
$$
\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{\cos \theta} & - \color{green}{\sin \theta} & \color{green}0 \\ \color{blue}0 & \color{blue}{\sin \theta} & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{green}{\cos \theta} \cdot y - \color{green}{\sin \theta} \cdot z \\ \color{blue}{\sin \theta} \cdot y + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}
$$
沿 y 軸旋轉
$$
\begin{bmatrix} \color{red}{\cos \theta} & \color{red}0 & \color{red}{\sin \theta} & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ - \color{blue}{\sin \theta} & \color{blue}0 & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x + \color{red}{\sin \theta} \cdot z \\ y \\ - \color{blue}{\sin \theta} \cdot x + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}
$$
沿 z 軸旋轉
$$
\begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}
$$

我們可以把三軸的旋轉組合起來，達成任意的旋轉，但這會產生:萬象鎖(Gimbal Lock)的問題產生

當第二個旋轉軸是 90 度時，會使得第一個旋轉軸與第三個旋轉軸等價，丟失了一個維度

這裡有很好的解釋

https://www.youtube.com/watch?v=zc8b2Jo7mno
https://www.youtube.com/watch?v=zjMuIxRvygQ
https://silverwind1982.pixnet.net/blog/post/345691427-gimbal-lock---%E8%90%AC%E5%90%91%E9%8E%96
https://krasjet.github.io/quaternion/quaternion.pdf
[ ] https://krasjet.github.io/quaternion/bonus_gimbal_lock.pdf
更好的模型是:沿著任意的軸，例如單位向量 $(0.662, 0.2, 0.7222)$，而不是拆成三個軸的選轉組合
- $(\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})$ 代表任意旋轉軸
- 但仍不能完全解決萬象鎖的問題
- 真正的解法是使用四元數(Quaternion)

$$
\begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
$$

矩陣組合

多個變換矩陣可以用乘法融合到一個矩陣中。例如，先縮放兩倍、再位移$(1,2,3)$
矩陣乘法是從最右邊開始，依序往左乘，所以是最右邊的操作最先發生。

$$
Trans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \\
\begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix}
$$

不同的操作之間可能相互影響，依照縮放、旋轉、位移的順序組合矩陣

GLM

OpenGL Mathematics，是一個 header-only 的 OpenGL 數學函式庫

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);

glm::mat4 trans(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
printf("%d %d %d\n", vec.x, vec.y, vec.z);

逆時針選轉 90 度，接著縮放 0.5 倍

1
2
3

glm::mat4 trans;
trans = glm::rotate(trans, glm::radian(90.f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));

矩陣乘法是反過來乘的，所以是先縮放再旋轉
修改 Vertex Shader ，新增 mat4

#version 450 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aVertColor;
layout (location = 2) in vec2 aTexCoord;

out vec3 VertColor;
out vec2 TexCoord;

uniform mat4 vTransform;

void main()
{
    gl_Position = vTransform * vec4(aPos, 1.0);
    TexCoord = aTexCoord;
    VertColor = aVertColor;
}

將矩陣傳到 Vertex Shader

1 2	int transformLoc = glGetUniformLocation(program, "vTransform"); glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

Example 5.1 Transformation

Lab
- 將應用在箱子上的最後一個變換，嘗試將其改變為先旋轉，後位移。看看發生了什麼，試著想想為什麼會這樣
  
  Ans
  
  因為矩陣運算是反過來的，所以如果 translate 後再 rotate ，原點就不在 (0, 0, 0) 上
  所以會像是繞 (0, 0) 旋轉
- 嘗試再次調用 glDrawElements 畫出第二個箱子，只使用變換將其擺放在不同的位置。讓這個箱子被擺放在窗口的左上角，並且會不斷的縮放（而不是旋轉）。
  
  Ans

Reference

https://ocw.chu.edu.tw/pluginfile.php/810/mod_resource/content/17/Summary_211.pdf

如果你覺得這篇文章很棒，請你不吝點讚 (ﾟ∀ﾟ)

r0yblog

存放一些有關程式、生活、心得隨筆的網誌